GEOMETRIA ANALÍTICA
Dados os vetores u(-5,3,4) e v(2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v).(2u - v).
-123
123
150
-277
277
Na figura a seguir tem-se uma elipse centrada na origem e possui os seus eixos sobre os eixos x e y do plano cartesiano. Analise as alternativas e assinale a que corresponde a equação desta elipse.

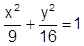
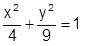
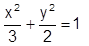
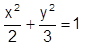
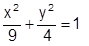
Seja o plano  . Calcule o ponto de π que tem abscissa 1 e ordenada 3.
. Calcule o ponto de π que tem abscissa 1 e ordenada 3.
(1, 3, 2)
(2, 1, 3)
(-6, 3, 1)
(2, 3, 1)
(3, 1, -6)
Encontre a equação geral para parábola de vértice V(4, 2) e foco F(1, 2).
y2 + 12x – 4y - 44 = 0
y2 - 4x – 12y - 48 = 0
y2 - 4x + 12y + 44 = 0
y2 + 12x – 4y - 52 = 0
y2 - 6x + 2 + 22 = 0
Um vetor para ser definido necessita de módulo, direção e sentido. Em muitos casos pode-se obter outros vetores a partir de um vetor dado, verificando a direção e o sentido. Com base no exposto, assinale a alternativa que expressa um vetor de mesma direção e mesmo sentido do vetor 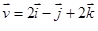 .
.
%7D)
%7D)
%7D)
%7D)
%7D)
Analise as afirmações feitas sobre a classificação das retas em concorrentes, paralelas coincidentes ou paralelas distintas.
I. Duas retas são concorrentes se possuem um ponto em comum.
II. Duas retas são paralelas se têm pontos em comum.
III. Duas retas que possuem entre si um ângulo de 90º são concorrentes.
IV. Duas retas são perpendiculares apenas se têm um único ponto comum.
V. As retas r: 6x + 7y+3=0 e s:12x+14y-21=0 são paralelas
Marque a alternativa que contém as afirmações verdadeiras:
Apenas I e II
Apenas I, III e V
I, II, III, IV e V
Apenas I, II e III
Apenas II, IV e V
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio igual a 3 e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(6, -9) e B(-2, 3).
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.
-123
123
150
-277
277
Na figura a seguir tem-se uma elipse centrada na origem e possui os seus eixos sobre os eixos x e y do plano cartesiano. Analise as alternativas e assinale a que corresponde a equação desta elipse.

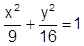
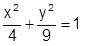
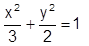
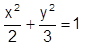
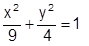
Seja o plano  . Calcule o ponto de π que tem abscissa 1 e ordenada 3.
. Calcule o ponto de π que tem abscissa 1 e ordenada 3.
(1, 3, 2)
(2, 1, 3)
(-6, 3, 1)
(2, 3, 1)
(3, 1, -6)
Encontre a equação geral para parábola de vértice V(4, 2) e foco F(1, 2).
y2 + 12x – 4y - 44 = 0
y2 - 4x – 12y - 48 = 0
y2 - 4x + 12y + 44 = 0
y2 + 12x – 4y - 52 = 0
y2 - 6x + 2 + 22 = 0
Um vetor para ser definido necessita de módulo, direção e sentido. Em muitos casos pode-se obter outros vetores a partir de um vetor dado, verificando a direção e o sentido. Com base no exposto, assinale a alternativa que expressa um vetor de mesma direção e mesmo sentido do vetor 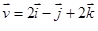 .
.
%7D)
%7D)
%7D)
%7D)
%7D)
Analise as afirmações feitas sobre a classificação das retas em concorrentes, paralelas coincidentes ou paralelas distintas.
I. Duas retas são concorrentes se possuem um ponto em comum.
II. Duas retas são paralelas se têm pontos em comum.
III. Duas retas que possuem entre si um ângulo de 90º são concorrentes.
IV. Duas retas são perpendiculares apenas se têm um único ponto comum.
V. As retas r: 6x + 7y+3=0 e s:12x+14y-21=0 são paralelas
Marque a alternativa que contém as afirmações verdadeiras:
Apenas I e II
Apenas I, III e V
I, II, III, IV e V
Apenas I, II e III
Apenas II, IV e V
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio igual a 3 e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(6, -9) e B(-2, 3).
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.

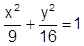
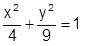
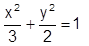
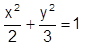
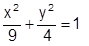
Seja o plano  . Calcule o ponto de π que tem abscissa 1 e ordenada 3.
. Calcule o ponto de π que tem abscissa 1 e ordenada 3.
(1, 3, 2)
(2, 1, 3)
(-6, 3, 1)
(2, 3, 1)
(3, 1, -6)
Encontre a equação geral para parábola de vértice V(4, 2) e foco F(1, 2).
y2 + 12x – 4y - 44 = 0
y2 - 4x – 12y - 48 = 0
y2 - 4x + 12y + 44 = 0
y2 + 12x – 4y - 52 = 0
y2 - 6x + 2 + 22 = 0
Um vetor para ser definido necessita de módulo, direção e sentido. Em muitos casos pode-se obter outros vetores a partir de um vetor dado, verificando a direção e o sentido. Com base no exposto, assinale a alternativa que expressa um vetor de mesma direção e mesmo sentido do vetor 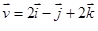 .
.
%7D)
%7D)
%7D)
%7D)
%7D)
Analise as afirmações feitas sobre a classificação das retas em concorrentes, paralelas coincidentes ou paralelas distintas.
I. Duas retas são concorrentes se possuem um ponto em comum.
II. Duas retas são paralelas se têm pontos em comum.
III. Duas retas que possuem entre si um ângulo de 90º são concorrentes.
IV. Duas retas são perpendiculares apenas se têm um único ponto comum.
V. As retas r: 6x + 7y+3=0 e s:12x+14y-21=0 são paralelas
Marque a alternativa que contém as afirmações verdadeiras:
Apenas I e II
Apenas I, III e V
I, II, III, IV e V
Apenas I, II e III
Apenas II, IV e V
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio igual a 3 e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(6, -9) e B(-2, 3).
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.
(1, 3, 2)
(2, 1, 3)
(-6, 3, 1)
(2, 3, 1)
(3, 1, -6)
Encontre a equação geral para parábola de vértice V(4, 2) e foco F(1, 2).
y2 + 12x – 4y - 44 = 0
y2 - 4x – 12y - 48 = 0
y2 - 4x + 12y + 44 = 0
y2 + 12x – 4y - 52 = 0
y2 - 6x + 2 + 22 = 0
Um vetor para ser definido necessita de módulo, direção e sentido. Em muitos casos pode-se obter outros vetores a partir de um vetor dado, verificando a direção e o sentido. Com base no exposto, assinale a alternativa que expressa um vetor de mesma direção e mesmo sentido do vetor 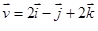 .
.
%7D)
%7D)
%7D)
%7D)
%7D)
Analise as afirmações feitas sobre a classificação das retas em concorrentes, paralelas coincidentes ou paralelas distintas.
I. Duas retas são concorrentes se possuem um ponto em comum.
II. Duas retas são paralelas se têm pontos em comum.
III. Duas retas que possuem entre si um ângulo de 90º são concorrentes.
IV. Duas retas são perpendiculares apenas se têm um único ponto comum.
V. As retas r: 6x + 7y+3=0 e s:12x+14y-21=0 são paralelas
Marque a alternativa que contém as afirmações verdadeiras:
Apenas I e II
Apenas I, III e V
I, II, III, IV e V
Apenas I, II e III
Apenas II, IV e V
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio igual a 3 e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(6, -9) e B(-2, 3).
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.
y2 + 12x – 4y - 44 = 0
y2 - 4x – 12y - 48 = 0
y2 - 4x + 12y + 44 = 0
y2 + 12x – 4y - 52 = 0
y2 - 6x + 2 + 22 = 0
Um vetor para ser definido necessita de módulo, direção e sentido. Em muitos casos pode-se obter outros vetores a partir de um vetor dado, verificando a direção e o sentido. Com base no exposto, assinale a alternativa que expressa um vetor de mesma direção e mesmo sentido do vetor 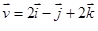 .
.
%7D)
%7D)
%7D)
%7D)
%7D)
Analise as afirmações feitas sobre a classificação das retas em concorrentes, paralelas coincidentes ou paralelas distintas.
I. Duas retas são concorrentes se possuem um ponto em comum.
II. Duas retas são paralelas se têm pontos em comum.
III. Duas retas que possuem entre si um ângulo de 90º são concorrentes.
IV. Duas retas são perpendiculares apenas se têm um único ponto comum.
V. As retas r: 6x + 7y+3=0 e s:12x+14y-21=0 são paralelas
Marque a alternativa que contém as afirmações verdadeiras:
Apenas I e II
Apenas I, III e V
I, II, III, IV e V
Apenas I, II e III
Apenas II, IV e V
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio igual a 3 e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(6, -9) e B(-2, 3).
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.
Analise as afirmações feitas sobre a classificação das retas em concorrentes, paralelas coincidentes ou paralelas distintas.
I. Duas retas são concorrentes se possuem um ponto em comum.
II. Duas retas são paralelas se têm pontos em comum.
III. Duas retas que possuem entre si um ângulo de 90º são concorrentes.
IV. Duas retas são perpendiculares apenas se têm um único ponto comum.
V. As retas r: 6x + 7y+3=0 e s:12x+14y-21=0 são paralelas
Marque a alternativa que contém as afirmações verdadeiras:
Apenas I e II
Apenas I, III e V
I, II, III, IV e V
Apenas I, II e III
Apenas II, IV e V
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio igual a 3 e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(6, -9) e B(-2, 3).
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.
Apenas I e II
Apenas I, III e V
I, II, III, IV e V
Apenas I, II e III
Apenas II, IV e V
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio igual a 3 e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(6, -9) e B(-2, 3).
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.
x2 - y2 + 2x - 6y – 4 = 0
x2 + y2 - 4x + 6y + 4 = 0
(x - 2)2 + (y + 3)2 = 9
(x + 4)2 + (y - 9)2 = 4
(x + 2)2 + (y - 3)2 = 9
Dados os vetores u = (4, -2) e v = (3, -2). Assinale a alternativa que corresponde ao vetor x de modo que 2(u – v) - 1/4x = u + 2x.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)
Assinale a alternativa que expressa a transformação da equação cartesiana 3x + 6y = 12 em uma equação polar.
x = (8/9, -8/9)
x = (8/9, 8/9)
x = (-8/9, 8/9)
x = (-8/9, -8/9)
x = (-9/8, 9/8)